1+1=4: Top Four (Peculiar Weave)

The premise of this week is simple: I’ll show you how to make four small cuddle quilts out of a single roll of 2.5″ strips and a yard of cuddle fabric or fleece. The final quilts measure 18″×24″, so these are meant for comfort more than sleeping under. Today, we’re making the final quilt top. If you’re just joining in, you may want to hop over to all posts tagged 1+1=4 or start from the beginning of the series.

This final top is something I call “Peculiar Weave”. Be very careful when cutting, as this top needs every millimeter of a 42″ strip. If your strips are less than 42″ long without selvage, you will need to make a second Top One or Top Two.

Cut each of the two remaining strip sets (A and B) into three 6.5″ segments (A6/B6) and nine 2.5″ segments.

Use six of the smaller segments from each to create nine-patches: two each, ABA (A3) and BAB (B3).

Use two more small segments from each to make an AB (A2) pair and a BA (B2) pair.

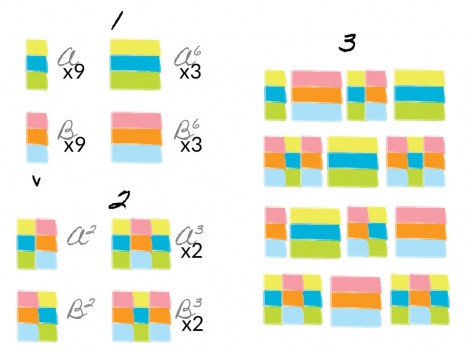
Create four rows:
A B6 A2 A6
B3 A6 B3
B A6 B2 B6
A3 B6 A3

Sew the four rows together in the above order. You’ll then have an 18.5″×24.5″ unfinished top.

Almost done! Stick around, and I’ll show you how to sew them into simple quilts.

1+1=4: 1 roll + 1 yard = 4 quilts for charity

Link up:
<a href="http://raevenfea.com/tag/1-plus-1-equals-4/" rel="external" title="Learn how to create these quilts"><img decoding="async" loading="lazy" src="http://raevenfea.com/media/1plus1equals4-280x280.png" border="0" width="240" height="240" alt="1+1=4: 1 roll + 1 yard = 4 quilts for charity"></a>

This post is part of a series on making small cuddle quilts for charity. My finished quilts will be donations to the 2012/13 service project being sponsored by the Quilter’s Consortium of New York State. If you’re in a NY quilt guild that is a member of QCNYS, contact your consortium rep to learn how to donate (and tell your guild or club about this series!). If you are not a member of a participating guild, but would still like to donate send me an email and we can figure out how to get the quilts to the right place.

2 Responses to “1+1=4: Top Four (Peculiar Weave)”

Koba

9:40 pm | 10/25/12

Am I correct in being reminded of algebraic weaving with these patterns?

http://fiberarts.org/design/articles/algebra.html
Rachael Arnold

10:49 am | 10/26/12

You give me far too much credit for wanting anything to do with algebra :p

But, it does seem that there might be a formula that can be derived from that, true.

Perhaps I will have to look into furthering the idea someday. The (a+b)^3 pattern is quite nice.